APPRILIA AGUSTI_50420206_Tugas M5 OSK

 

APPRILIA AGUSTI

50420206

2IA19

 

1.       Apa yang di maksud teori de morgan,berikan contohnya

Jawab :

Pembuktian Hukum de Morgan

Hukum de Morgan

Dalil 1 hukum de morgan menyatakan bahwa komplemen dari hasil penjumlahan akan sama dengan hasil perkalian dari masing masing komplemen.Teori ini melibatkan gerbang NOR dan AND.

Dalil II hukum de morgan menyatakan bahwa komplemen dari hasil perkalian akan sama dengan hasil penjumlahan dari masing masing komplemen.Teori ini melibatkan gerbang NAND dan OR

Dari hukum De Morgan dapat disimpulkan, bahwa untuk mendapatkan komplemen (pelengkap) dari suatu fungsi boole adalah dengan mengubah semua operasi OR menjadi operasi AND, ataupun sebaliknya mengubah semua operasi AND menjadi operasi OR, dan melakukan penolakan masing-masing simbol binernya. Dan dengan pertolongan hukum De Morgan dapat kita tunjukkan bahwa suatu rangkaian AND untuk logika positif juga bekerja seperti halnya suatu gerbang OR untuk logika negatif.

Hukum De Morgan dalam teori Himpunan Klasik termasuk hukum yang sangat bermanfaat dan banyak digunakan dalam Aljabar Boolean, Logika Matematika, atau Rangkaian Logika untuk mendapatkan ekivalens dari suatu ekspresi himpunan atau ekspresi logika. Hukum De Morgan sudah terbukti atau diakui keberlakuannya dalam Himpunan Klasik. Pada kesempatan tulisan kali ini, akan dicoba pengujian keberlakuan Hukum De Morgan dalam Himpunan Fuzzy sehingga dapat dianggap Generalized De Morgan.

Pengujian keberlakuan Hukum De Morgan dalam Himpunan Fuzzy akan dilakukan menggunakan 4-operator (Min/Max, Algebraic, Bounded, Drastic) masing-masing untuk T-norm (irisan atau konjungsi) maupun T-conorm (gabungan atau disjungsi) serta satu operator untuk Negasi (komplemen) yaitu komplemen klasik Zadeh, yaitu  atau N(a) = 1 – a. Pengujian dilakukan menggunakan Matlab dengan setiap operator dibuatkan fungsi atau prosedur dalam kode bahasa Matlab.

Hukum De Morgan yang diujikan adalah T(a,b) = N(S(N(a),N(b))) dan S(a,b) = N(T(N(a),N(b))), dengan T adalah operator T-norm, S adalah operator S-norm atau T-conorm, dan N adalah Komplemen Klasik Zadeh, sedangkan “a” dan “b” adalah derajad keanggotaan Himpunan Fuzzy. Dari keseluruhan (delapan) pengujian yang dilakukan dalam penelitian ini, didapat hasil bahwa keempat operator (Min/Max, Algebraic, Bounded, Drastic) dan komplemen Klasik Zadeh berlaku diterapkan pada Hukum De Morgan.

Rumus-rumus di bawah ini yang merupakan rumus De' Morgan adalah

(A U B)' = A' U B' b. (A n B)' = A' n B' c. A' U B'=A' U B' d. (A u B)' =A' n B'

 

Contoh Hukum De Morgan

Sebagai contoh, pertimbangkan himpunan bilangan real dari 0 sampai 5. Kami menulis ini dalam notasi interval [0, 5]. Dalam himpunan ini kita memiliki A = [1, 3] dan B = [2, 4]. Selanjutnya, setelah menerapkan operasi dasar, kami memiliki:

·       Komplemen A ^C = [0, 1) U (3, 5]

·       Komplemen B ^C = [0, 2) U (4, 5]

·       Serikat A U B = [1, 4]

·       Persimpangan A  ∩ B = [2, 3]

Kita mulai dengan menghitung serikat  A ^C U B ^C . Kita melihat bahwa gabungan [0, 1) U (3, 5] dengan [0, 2) U (4, 5] adalah [0, 2) U (3, 5]. Perpotongan A  ∩ B adalah [2 , 3]. Kita melihat bahwa komplemen dari himpunan ini [2, 3] juga [0, 2) U (3, 5]. Dengan cara ini kita telah menunjukkan bahwa A ^C U B ^C = ( A  ∩ B ) ^C .

Sekarang kita melihat perpotongan [0, 1) U (3, 5] dengan [0, 2) U (4, 5] adalah [0, 1) U (4, 5]. Kita juga melihat bahwa komplemen dari [ 1, 4] juga [0, 1) U (4, 5]. Dengan cara ini kami telah menunjukkan bahwa A ^C  ∩ B ^C = ( A U B ) ^C .

2.       Apa itu Kmap dan bagaimana teknik Kmap/Karnaugh Map (minimasi)

Jawab :

Karnaugh Map atau K-Map adalah suatu teknik penyederhanaan fungsi logika dengan cara pemetaan. K-Map terdiri dari kotak-kotak yang jumlahnya terdiri dari jumlah variable dan fungsi logika atau jumlah inputan dari rangkaian logika yang sedang kita hitung.

Langkah – Langkah menggunakan Kmap

1.     Konversikan persamaan Boolean yang diketahui ke dalam bentuk persamaan SOP-nya (Sum of Product). Gunakan Tabel Kebenaran sebagai alat bantu.

2.     Gambarlah K-map, dengan jumlah sel = 2 ^ jumlah variabel input.

3.     Isi sel K-map sesuai dengan minterm pada Tabel Kebenaran.

4.     Cover minterm-minterm bernilai 1 yang berdekatan, dengan aturan :

a.     hanya minterm berdekatan secara vertikal atau horizontal yang boleh di-cover.

b.     Jumlah minterm berdekatan yang boleh di-cover adalah : 2. 4, 8, 16, 32

5.     Buat persamaan SOP baru sesuai dengan hasil peng-cover-an minterm.

 

Penyederhanaan Dua Variabel

Catatan : Bar = ‘

Tabel dari K-Map 2 variabel adalah seperti dibawah ini

Contoh Soal :

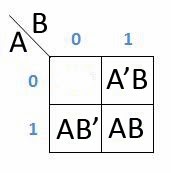
H = AB + A’B+AB’

Maka cara pengerjaanya seperti dibawah ini

Bar (‘) atau aksen biasanya ditulis kedalam angka 0 sedangkan angka 1 adalah tanpa Bar aksen.

Dan dapat dipermudah lagi menjadi dibawah ini :

Yang dapat disederhanakan dalam K-Map hanya 2 / kelipatan 2 dari kotak yang berdempetan dan sedangkan jika seperti kotak diatas maka penyderhanaannya:

Karena kolom ber angka 1 dan baris ber angka 1 memenuhi setiap garisnya, maka dapat disimpulkan kalau H = AB + A’B+AB’ K-Map nya adalah AB/BA

Penyederhanaan Tiga Variabel

Catatan : Bar = ‘

Tabel dari K-Map 3 variabel adalah seperti dibawah ini

Contoh Soal

H = ABC + A’BC+A’B’C+AB’C

Maka cara pengerjaanya seperti dibawah ini

Dan dapat dipermudah lagi menjadi dibawah ini

Sekarang kita lihat, karena yang memenuhi setiap kotaknya adalah baris 01 dan 11 sedangkan simbol 01 artinya adalah (B’C) dan 11 artinya adalah (BC) dan simbol yang tidak ada aksen nya hanya C, maka H = ABC + A’BC+A’B’C+AB’C adalah C.

Penyederhanaan 4 variabel

Catatan : Bar = ‘

Tabel dari K-Map 4 variabel adalah seperti dibawah ini :

Contoh Soal

H = ABCD + ABCD’+AB’CD+ABC’D’

Maka cara pengerjaanya seperti dibawah ini

Dan dapat dipermudah lagi menjadi dibawah ini :

Karena yang ada angka 1 nya ada di kolom dan baris 1100, 1111, 1110 dan 1011, yaitu AB, ABCD, ABC dan ACD maka jika kita eliminasi dengan cara mengambil huruf yang sama saja menjadi AB + ABC + ACD.

3.       Gerbang Logika

Jawab :

Fungsi Gerbang Logika

Fungsi sistem gerbang logika (logic gate) adalah sebagai perintah atau penerjemah, dimana ia menghubungkan banyak perangkat atau komponen di dalamnya. Mulai dari IC (Integrated Circuit), Transistor, Dioda, Optik, Relay, dan beragam perangkat elektronik lainnya.

Umumnya dalam sebuah chip alat elektronik mempunyai jutaan sistem gerbang ini, setiap gerbangnya memiliki tujuan atau fungsi berbeda. Namun secara garis besar ia dapat dikelompokkan menjadi beberapa rangkaian, mulai flip-flop, counter, multiplexer, demultiplexer, dan lain sebagainya.

Jenis-jenis Gerbang Logika

Sedangkan untuk jenis-jenisnya sistem gerbang ini memiliki 7 jenis yang paling utama, setiap jenis memiliki fungsi serta cara kerja yang berbeda-beda. 

Selain itu penggunaannya juga disesuaikan dengan kebutuhan, karena setiap sistem mempunyai rangkaian input dan output yang berbeda-beda. Untuk lebih lengkapnya berikut ini adalah ulasan yang bisa Anda simak :

 

 

 

 

1. Gerbang AND (AND Gate)

Gerbang AND termasuk yang paling sederhana diantara lainnya, dimana gerbang ini membutuhkan dua input untuk menghasilkan satu output. Sistemnya terdiri dari 0 dan 0 akan menghasilkan 0, 1 dan 0 akan menghasilkan 0, 1 dan 1 akan menghasilkan 1.

Dari konfigurasi tersebut terciptalah sebuah input dan output sederhana, biasanya ia digunakan untuk sebuah IC alat elektronik seperti TTL Logic AND Gate atau CMOS Logic AND Gate.

2. Gerbang OR (OR Gate)

Selanjutnya terdapat Gerbang OR atau OR Gate, gerbang ini sebenarnya hanya berbeda sedikit dari AND. Karena ia memiliki konfigurasi input 0 dan 0 akan menghasilkan 0, 0 dan 1 akan menghasilkan 1, 1 dan 0 akan menghasilkan 1, lalu 1 dan 1 akan menghasilkan 1.

 

Gerbang ini biasa digunakan untuk melengkapi sebuah sistem digital, dimana ia berfungsi agar sistem digital memiliki opsi yang lebih luas terhadap sistem geraknya. Terutama saat digunakan di samping Gerbang AND yang merupakan opsi lain dari gerbang yang satu ini.

3. Gerbang NOT (NOT Gate) atau Inverter

Disebut juga sebagai Inverter (pembalik), Gerbang NOT memang memiliki konfigurasi terbalik. Ia dapat mengubah input 0 menjadi output 1, sedangkan input 0 akan menjadi output 1. Gerbang NOT juga sangat berbeda dengan gerbang lainnya, karena ia hanya mempunyai 1 input dan 1 output saja.

 

Umumnya Gerbang NOT di simbolkan dengan lambang (-) diatas variabel lainnya, hal tersebut bertujuan agar penggunaannya tidak salah atau keliru. Hal ini karena ia berguna sebagai pembalik dan berfungsi sangat vital dalam sistem digital.

4. Gerbang NAND (NAND Gate)

Gerbang logika berikutnya ialah Gerbang NAND atau bisa disebut Non AND, karena konfigurasi yang dimilikinya berlawanan dengan Gerbang AND. Sehingga penggunaannya juga sangatlah berbeda.

Gerbang NAND dapat mengubah input 0 dan 0 menjadi output 1, 0 dan 1 menjadi output 1, 1 dan 0 menjadi outpout 1, lalu 1 dan 1 menjadi output 0

 

5. Gerbang NOR (NOR Gate)

Selanjutnya gerbang yang menjadi kebalikan dari Gerbang OR, yaitu Gerbang NOR (Not OR).Gerbang ini sendiri memiliki tabel kebenaran input 0 dan 0 menjadi output 1, 0 dan 1 menjadi output 0, 1 dan 0 menjadi output 0, lalu 1 dan 1 menjadi output 0.

 

Dari konfigurasi tersebut membuatnya sangat berlawanan dengan Gerbang OR, sehingga bisa juga dipakai untuk menambah opsi dalam pemasangan sistem digital.

6. Gerbang X-OR (X-OR Gate)

Ada juga versi Gerbang X-OR atau bisa disebut Exclusive OR, seperti namanya ia adalah versi pengembangan dari Gerbang OR. Konfigurasinya sendiri terdiri dari input 0 dan 0 menjadi 0, 0 dan 1 menjadi output 1, 1 dan 0 menjadi 1, lalu 1 dan 1 menjadi 0.

Sistem baru ini digunakan untuk menjadi opsi yang lebih luas dalam penggunaan, sehingga sistem digital dapat lebih memiliki banyak pilihan dalam operasionalnya.

7. Gerbang X-NOR (X-NOR Gate)

Sama dengan gerbang lainnya, Gerbang X-NOR juga memiliki konfigurasi dua input dan satu output. Bedanya ia sendiri merupakan pengembang dari Gerbang NOR, sehingga ia dinamai Exclusive NOR.

Seperti nama yang diberikan, konfigurasi gerbang ini adalah pengembangan konfigurasi Gerbang NOR. Lebih tepatnya ia memiliki input 0 dan 0 akan menghasilkan 1, 0 dan 1 akan menghasilkan 0, 1 dan 0 akan menghasilkan 0, lalu 1 dan 1 akan menghasilkan 1.

Konfigurasinya menganut sistem logika dasar aljabar positif, dimana angka sama akan dapat terhubung dan menghasilkan keluaran 1. Sedangkan angka berbeda akan menganut salah satu angka, disini sendiri ia akan menjadi keluaran berupa 0.

Simbol Gerbang Logika

Setiap jenis gerbang mempunyai simbol serta tabel yang berbeda, baik dari input maupun outputnya, sistem konfigurasi, hingga rangkaian yang dimilikinya. Hal tersebut akan mempermudah penggunaan serta penerapannya dalam sebuah sistem digital.

Secara umum simbol Logic Gate berupa A dan B, sedangkan untuk tabel input dan output disimbolkan dengan A, B, dan Y. Sehingga ia dapat dengan mudah diaplikasikan pada sistem elektronik apapaun, untuk lebih lengkapnya Anda bisa menyimak gambar berikut ini :

 

 

Sistem Logic Gate memang sangatlah sederhana, namun komponen ini mempunyai peran penting dalam sebuah sistem digital. Dimana dalam sistem digital elektronik sendiri, jumlah gerbang yang digunakan bisa mencapai jutaan pasang. Sehingga dapat memiliki sistem berbeda-beda setiap penggunaannya.